Design attributes for plane

We already know we’re going to need to use a fixed-wing body in order to achieve the sort of range we’re shooting for with this plane. Now let’s do a few behind-the-napkin calculations to narrow the range of options down to something manageable.

The few hours we spend doing calculations now will save us a lot of time later as we try to pick a suitable frame for the mission. Specifically, we’ll try to determine the minimum size and power requirements in order to achieve the 30km x 2 milestone trip we’re working towards.

I have no aerodynamics background, so I’ll be reading a lot of this time from various online resources. This will involve a bunch of research and a lot of calculating — I’ll share my sources and proof as we go along.

Previous work

Before we hit the theoretical section, it’s good to have a grasp of what’s already been achieved — just so we have some sort of practical baseline for our expectations.

Here’s what a bit of researching turned up:

Range	Wing span	Weight	Battery	Frame
80km	2.5m	3.5kg	20,000mAh	Flying wing w/solar
200km	2.24m	5kg	2x16,000mAh	Fixed wing, MTD mod
100km	1.9m	?	4x5,000mAh	Flying wing, Skywalker X7

Theory

I did some searching through a relevant technical paper and came up with the following:

Lift / Thrust

At level flight (which is where our plane will spend most of its time), the lift generated by the plane should equal the weight of the plane. The thrust from the motor is used to overcome the drag that results from the plane’s movement through the air. This looks like:

\[\text{Weight} = F_L = C_{L_a}\rho S \frac{V^2}{2}\] \[\text{Thrust} = F_D = C_{D_a}\rho S \frac{V^2}{2}\]

where \(\rho\) is the air density, \(S\) is the wing area, \(V\) is the airspeed

To calculate the actual power required to achieve level flight, we use:

\[P_\text{level} = F_D V = C_{D_a} C_{L_a}^{-\frac{3}{2}} F_L^\frac{3}{2} \left(\frac{\rho S}{2}\right)^{-\frac{1}{2}}\]

One consideration we need to make when calculating the power required for level flight is the efficiency of the matched components (propeller, gearbox, motor and the controller):

\[P_\text{actual} = \frac{P_\text{level}}{ \eta_\text{ppl} \eta_\text{gb} \eta_\text{mtr} \eta_\text{mctrl}}\]

with each of the efficiences \(0 \lt \eta \le 1\)

Drag

For the coefficient of drag \(C_{D_a}\), we can find

\[C_{D_a} = C_{D_0} + C_{D_{Lv}} + C_{D_{Li}}\]

where \(C_{D_0}\) is parasitic drag (which is form + skin friction + interference drag), \(C_{D_{Lv}}\) is separation drag, \(C_{D_{Li}}\) is lift induced drag

For a planar wing with elliptical lift distribution:

\[C_{D_{Li}} = \frac{C_{L_a}^2}{\pi e AR}\]

Where \(e\) is the Oswald efficiency number, \(AR\) is the aspect ratio of the wing.

To calculate the wing Aspect Ratio, we simply do \(\text{Aspect Ratio} = \frac{b}{c}\) where \(b\) is the wing span, \(c\) is chord

So?

While I still don’t know (after several hours of searching) enough about aerodynamics to be able to tell you exactly what the parameters need to be in order to support a trip with such distance, here are a few guidelines I was able to obtain from the above relationships:

1. \(P_\text{level} \propto \frac{C_{D_a}}{\sqrt{C_{L_a}^3}} \). Our job is to minimize \(P_\text{level}\) while achieving the minimum lift required in order to keep the plane in the air, which is \(W\)
2. The Lift/Drag curve is what determines how efficiently a plane is able to attain lift, and at what power draw. I wasn’t able to attain a minimum dimension like I hoped for (e.g. wing span must be greater than 1.5m) but I did understand how the different factors influence each other.

Buying the plane

From our research though, it’s clear that the MTD (MyTwinDream) is easily capable of meeting the requirements for this flight. I even verified this by asking a Youtuber that had one:

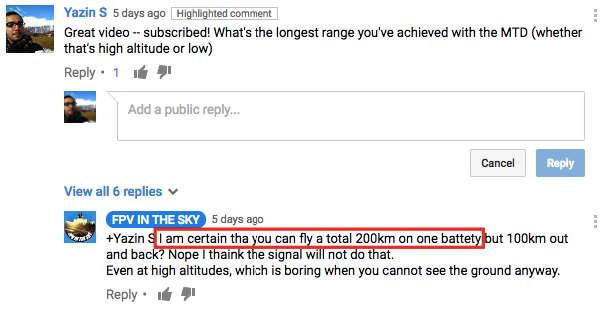
I’ve gone ahead and ordered one. Since it’ll take a few weeks to get here from China, we’ll talk about running some smaller scale tests in the mean time. Next up, we’ll pick a body for immediate testing.